{競艇解析} 階層ベイズモデルによる着順予測(2)

階層ベイズモデルによる着順予測(1)で階層ベイズモデルをたてました。
今回はそのモデルを実際に動かしてサンプリングされたパラメータをチェックしていきます。

strawberry-kyon.hateblo.jp
前回、モデルはこんな感じに立てました。
${\begin{eqnarray} &&Performance[g,r] \sim {\rm Normal}(\mu_n[n[g,r]]+\mu_c[c[g,r]],\sigma_p)\\ &&Performance[g,1]>Performance[g,2]>,...,>Performance[g,6]\\ &&\mu_n[n] \sim {\rm Normal}(0,\sigma_{\mu_n})\\ &&\sigma_p =10 \end{eqnarray}}$
$g,r,n$ はそれぞれ、レース、順位、選手のインデックスです。
このモデルからサンプリングして直接分かることは、艇番号の強さと各選手の強さです。
何号艇が強いか、どの選手が強いか弱いか、です。

対象データ・サンプリング方法

対象データは2013年1月1日から2017年6月30日の240460サンプル(不成立や欠損データは除く)です。
そのうち後ろから10000サンプルはテストデータとします。
サンプル内での選手数は1810人です。
サンプリングにはADVI(自動変分ベイズ、vb関数)を用いました。
データをstanへ読み込むために整えて、ぶん回します。

結果・考察

まずは、各艇番号における強さを表す $\mu_c$ から。
$\mu_c$ が大きい艇番号が強いことになります。
f:id:strawberry_kyon:20171006135730p:plain

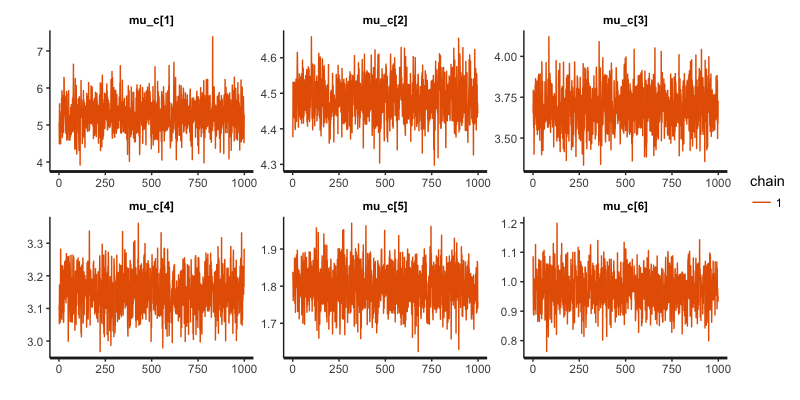
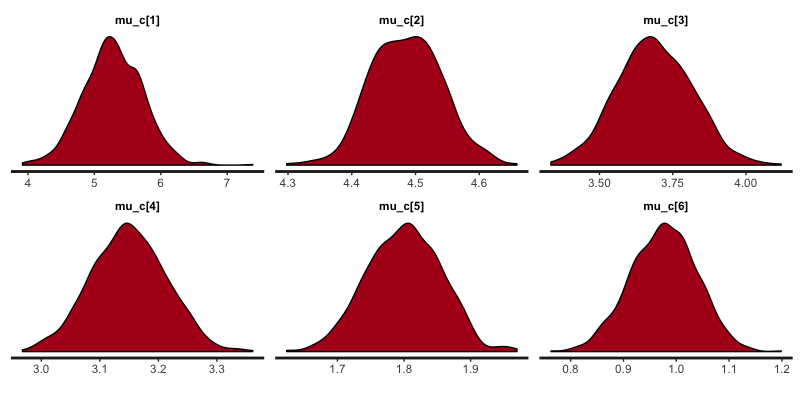
良い感じですね、直感と一致します。収束もしてそうです。
競艇は明らかに1号艇から6号艇にかけて不利になります。
モデルのパラメータもそのようになってとりあえず一安心です。
そういえば、選手のパフォーマンスの標準偏差を10に固定していました。
$\mu_c$ のオーダーもこれくらいで妥当な感じがします。

続いて、 $s_{\mu_n}$ を見てみます。
f:id:strawberry_kyon:20171006135732p:plain

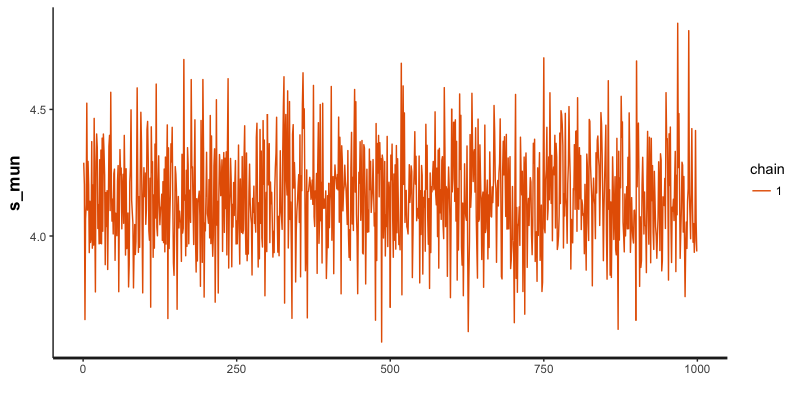
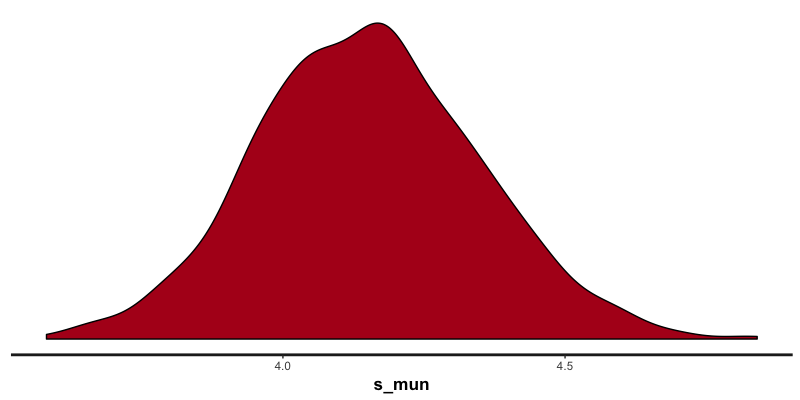
こちらも問題なく収束してそうですね。
どう考察すれば良いか難しいです。
値もこのくらいで良さそうとしか言えません。

続いて、 $\mu_n$ を見てみます。
$\mu_n$ は1810個あり全部を可視化してもあれなので、100個ランダムに選んで可視化します。
f:id:strawberry_kyon:20171006140520p:plain
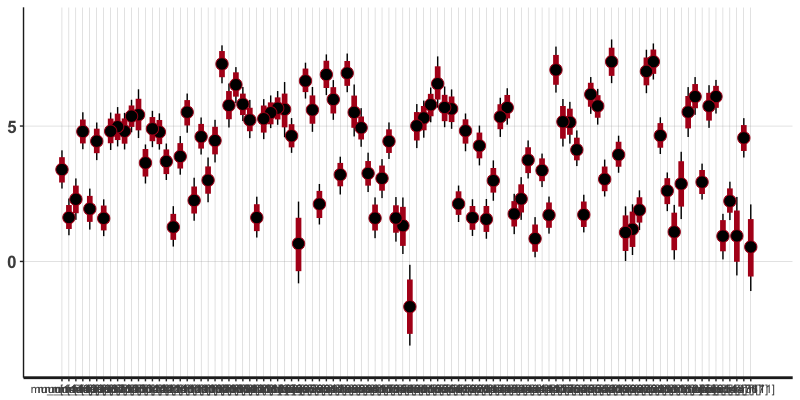
真ん中の点は中央値、バーは80%区間、線は95%区間です。
強い選手弱い選手いろいろいますね。
だいたいどの選手もばらつきは同じくらい。ばらつきが大きい選手は新人でしょうか。
$\mu_n$ はその選手の真の強さとしたいので、 $\mu_n$ があまりにばらつくならパフォーマンスの標準偏差を選手ごとに異なると仮定した方が良いかもしれませんね。
というよりそっちのが自然ですね。
$\mu_n$ がマイナスの選手もいますが、その選手はわざと負けているとかではないです。
$\mu_n$ は間隔尺度なので0とかプラスとかマイナスに意味はないです。
$\mu_n$ の中央値の大きい人50人と小さい人50人を見てみます。

No	Player_ID	Name	Rank	median
1	3573	前本泰和マエモトヤスカズ	A1	8.03796
2	3257	田頭実タドウミノル	B1	7.62809
3	3290	倉谷和信クラタニカズノブ	A1	7.61144
4	3159	江口晃生エグチアキオ	A1	7.60785
5	4061	萩原秀人ハギハラヒデト	A1	7.53984
6	4044	湯川浩司ユカワコウジ	A1	7.53828
7	3887	鎌田義カマダタダシ	B2	7.5319
8	2992	今村豊イマムラユタカ	A1	7.51819
9	3826	村田修次ムラタシユウジ	A1	7.48221
10	4102	益田啓司マスダケイジ	A1	7.46189
11	4366	前沢丈史マエザワタケシ	A1	7.44731
12	3849	中岡正彦ナカオカマサヒコ	A1	7.42436
13	4099	吉永則雄ヨシナガノリオ	A1	7.41935
14	4025	山本隆幸ヤマモトタカユキ	A1	7.41469
15	3554	仲口博崇ナカグチヒロタカ	A1	7.40151
16	3898	平田忠則ヒラタタダノリ	A1	7.38934
17	3959	坪井康晴ツボイヤスハル	A1	7.38063
18	4444	桐生順平キリュウジュンペイ	A1	7.37954
19	3256	三角哲男ミスミテツオ	A1	7.37619
20	3388	今垣光太郎イマガキコウタロウ	A1	7.37521
21	3795	金子龍介カネコリユウスケ	A1	7.34853
22	3909	佐々木康幸ササキヤスユキ	A1	7.34646
23	3780	魚谷智之ウオタニトモユキ	A1	7.31089
24	4238	毒島誠ブスジママコト	A1	7.30761
25	3940	飯山泰イイヤマヤスシ	A1	7.3055
26	4290	稲田浩二イナダコウジ	A1	7.30318
27	3737	上平真二ウエヒラシンジ	A1	7.29607
28	4237	大峯豊オオミネユタカ	A1	7.29178
29	3853	岩崎正哉イワサキマサヤ	A1	7.2865
30	4397	西村拓也ニシムラタクヤ	A1	7.2772
31	3623	深川真二フカガワシンジ	A1	7.25805
32	4028	田村隆信タムラタカノブ	A1	7.24669
33	3984	坂口周サカグチメグル	A2	7.24177
34	3502	渡邉英児ワタナベエイジ	A1	7.24103
35	3952	中澤和志ナカザワカズシ	A1	7.23507
36	3719	辻栄蔵ツジエイゾウ	A1	7.21356
37	3822	平尾崇典ヒラオタカノリ	A1	7.20069
38	4089	妹尾忠幸セノオタダユキ	A1	7.17875
39	4547	中田竜太ナカダリュウタ	A1	7.15994
40	3978	齊藤仁サイトウジン	A1	7.14737
41	4075	中野次郎ナカノジロウ	A1	7.13626
42	3966	作間章サクマアキラ	A1	7.13333
43	3010	大嶋一也オオシマカズヤ	A1	7.12934
44	3746	岡瀬正人オカセマサト	A1	7.12235
45	4208	三浦永理ミウラエリ	A1	7.10227
46	4150	山田雄太ヤマダユウタ	A1	7.09866
47	3635	石田政吾イシダセイゴ	A1	7.09552
48	4276	鈴木勝博スズキカツヒロ	A1	7.08698
49	4166	吉田拡郎ヨシダカクロウ	A1	7.08686
50	3473	石川真二イシカワシンジ	A1	7.08577
No	Player_ID	Name	Rank	median
1761	4960	黒野元基クロノモトキ	B2	-1.0812
1762	4894	原村拓也ハラムラタクヤ	B2	-1.09303
1763	4929	梅内夕貴奈ウメナイユキナ	B2	-1.11783
1764	4807	岡悠平オカユウヘイ	B2	-1.11788
1765	4982	中村将隆ナカムラノブタカ	B2	-1.14789
1766	4902	山川雄大ヤマカワタカヒロ	B1	-1.14837
1767	4946	船越健吾フナコシケンゴ	B2	-1.1528
1768	4840	鈴木秀茉スズキシュウマ	B1	-1.15309
1769	4868	松本峻マツモトシュン	B1	-1.16134
1770	4955	福田慶尚フクダケイショウ	B2	-1.16416
1771	4820	上野励ウエノレイ	B1	-1.17418
1772	4965	福岡泉水フクオカイズミ	B2	-1.18226
1773	4830	勝又桜カツマタサクラ	B1	-1.19162
1774	4957	竹之内極タケノウチキワム	B2	-1.19666
1775	4951	新田洋一ニッタヨウイチ	B2	-1.2006
1776	4942	柴田朋哉シバタトモヤ	B2	-1.20696
1777	4616	小川真人オガワマサト	B2	-1.20929
1778	4755	山田貴愛ヤマダタカアキ	B2	-1.24929
1779	4859	染川直哉ソメカワナオヤ	B1	-1.25615
1780	4953	尾上雅也オノウエマサヤ	B2	-1.27038
1781	4481	前田梓マエダアズサ	B2	-1.27293
1782	4956	齊藤大将サイトウヒロマサ	B2	-1.32408
1783	4858	須田大輝スダダイキ	B2	-1.34651
1784	4865	立具敬司タテグケイジ	B2	-1.35271
1785	4917	岩橋裕馬イワハシユウマ	B2	-1.3599
1786	4767	米井里実ヨネイサトミ	B2	-1.37628
1787	4898	菊地敬介キクチケイスケ	B1	-1.41652
1788	4768	田代元気タシロゲンキ	B2	-1.42259
1789	4986	西山祐希ニシヤマユウキ	B2	-1.42561
1790	4952	吉武真也ヨシタケシンヤ	B2	-1.43483
1791	4947	間庭菜摘マニワナツミ	B2	-1.48483
1792	4806	佐藤享子サトウキョウコ	B2	-1.51763
1793	4920	桐村翔太キリムラショウタ	B2	-1.53057
1794	4132	森年省吾モリトシセイゴ	B2	-1.53276
1795	4647	磯部温志イソベアツシ	B2	-1.53835
1796	4781	西舘果里ニシダテミサト	B2	-1.54974
1797	4869	寺垣光テラガキヒカリ	B2	-1.57476
1798	4940	白石有美シライシアミ	B2	-1.59303
1799	3520	岩本豊志イワモトトヨシ	B2	-1.60642
1800	4918	川島拓郎カワシマタクロウ	B2	-1.62562
1801	4613	竹内吉弘タケウチヨシヒロ	B2	-1.66523
1802	3758	津川和郎ツガワカズオ	B2	-1.67257
1803	4915	彦坂径冶ヒコサカケイヤ	B2	-1.73945
1804	4923	末武里奈子スエタケリナコ	B2	-1.77181
1805	4922	小林祐介コバヤシユウスケ	B2	-1.78251
1806	3004	早川清一ハヤカワキヨカズ	B2	-1.79629
1807	4810	後藤麦ゴトウムギ	B2	-1.93486
1808	4412	大原由子オオハラユウコ	B2	-2.04644
1809	3821	菊原隆司キクハラタカシ	B2	-2.0859
1810	4721	金光佑治カネミツユウジ	B2	-2.38298

上の方はA1が目立ち下の方はB2が目立ちますね。いい感じじゃないでしょうか。
前本泰和選手だけ飛び抜けてますね。有名な選手ですか？
調べてみると、目立つタイプの選手というより誰もが認める実力者みたいな選手の様ですね。
ここで、競艇の選手についてもっと詳しいと良い考察ができるのですが、私は詳しくないです。

一番強いとされた前本泰和選手と一番弱いとされた金光佑治選手を戦わせて見たいと思います。
選手の強さ $\mu_n$ と艇番号の強さ $\mu_c$ は中央値を用います。
前本泰和選手が1号艇で金光佑治選手が6号艇のときを想定します。
このとき、Performanceの密度はこんな感じになりました。
f:id:strawberry_kyon:20171006140521p:plain
割と被っているように見えますが、前本泰和選手が勝つ確率は85%くらいあります。
続いて、前本泰和選手が6号艇で金光佑治選手が1号艇のときを想定します。

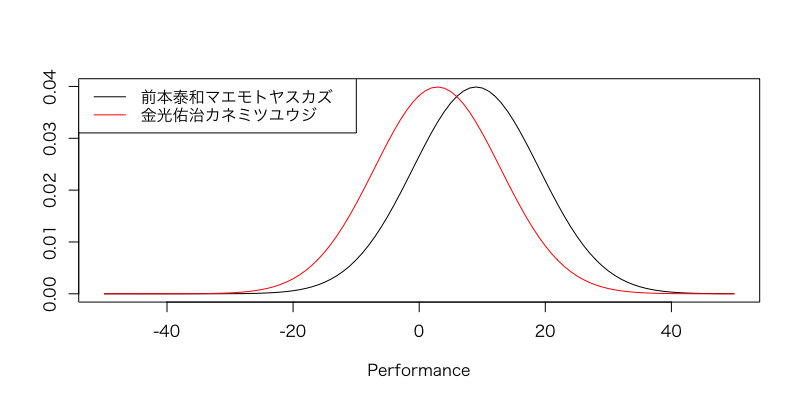
さらに被りましたが、前本泰和選手が勝つ確率は67%くらいあります。
実際どんなもんなんでしょう。こんなもんなんでしょうか。

では次に、予測の方に移りたいと思います。
サンプリングされたpeNから予測がどんなもんか見てみます。
6艇のPerformanceをサンプリングするので、1着から6着まで予測ができますが、周辺化して2着までの予測とします。

		2-1	0.0338	3-1	0.0335	4-1	0.0333	5-1	0.0333	6-1	0.0332
1-2	0.0336			3-2	0.0335	4-2	0.0334	5-2	0.0334	6-2	0.0334
1-3	0.0335	2-3	0.0338			4-3	0.0333	5-3	0.0332	6-3	0.0331
1-4	0.0335	2-4	0.0336	3-4	0.0333			5-4	0.0332	6-4	0.0329
1-5	0.0334	2-5	0.0336	3-5	0.0332	4-5	0.0331			6-5	0.0329
1-6	0.0333	2-6	0.0335	3-6	0.0332	4-6	0.0330	5-6	0.0329

表の見方は、例えば2-5の0.0336は1着と予測した艇が2着で2着と予測した艇が5着に来た割合です。
testデータの全レースまとめています。
ひどい結果になりましたね。ほとんど一様です。
適当にレース選んでPerformanceの分布を見てみます
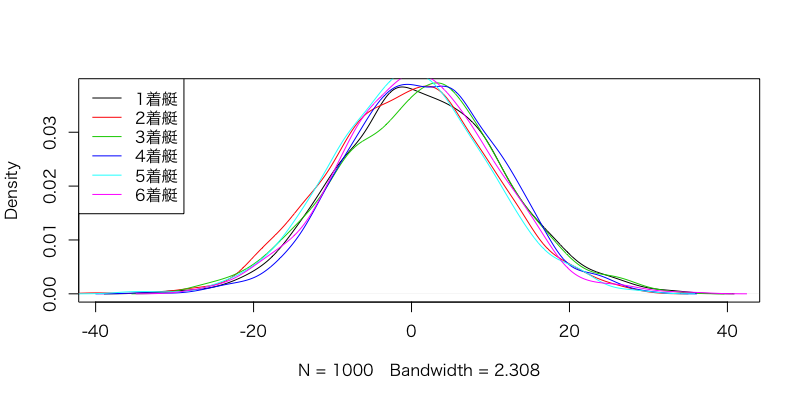
f:id:strawberry_kyon:20171006165916p:plain

f:id:strawberry_kyon:20171006165916p:plain

ほとんど被っちゃってます。これはよくないですね。
Performanceをサンプリングする前の、 $\mu_n[n[g,r]]+\mu_c[c[g,r]]$ の中央値を見てみます。

1着艇	2着艇	3着艇	4着艇	5着艇	6着艇
10.646	10.259	7.652	7.065	7.253	5.636

思ったより差がありますね。どういうことでしょうか。
この値を平均値、標準偏差=10とした正規分布の密度関数を描いてみます。
f:id:strawberry_kyon:20171006171227p:plain

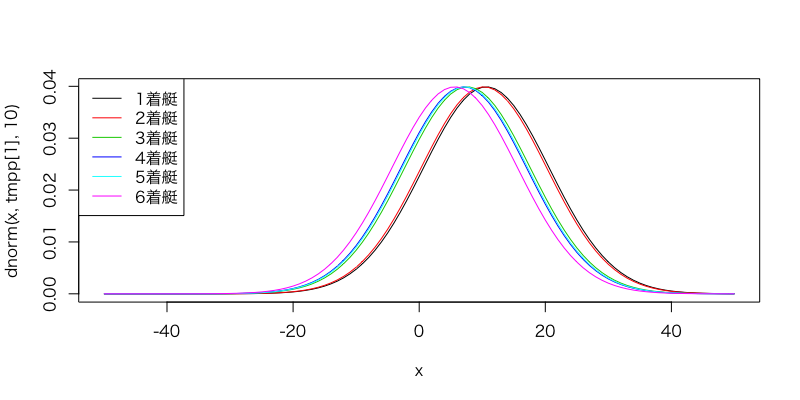
こんなもんなんですね。
着順の予測が分布として得られると、オッズと比較して期待値を推定できると思ったのですが、とりあえずこの方法では諦めます。
上の正規分布から改めてサンプリングし直してみます。

		2-1	0.0616	3-1	0.0388	4-1	0.0348	5-1	0.0357	6-1	0.0266
1-2	0.0630			3-2	0.0374	4-2	0.0347	5-2	0.0348	6-2	0.026
1-3	0.0474	2-3	0.0424			4-3	0.0251	5-3	0.0268	6-3	0.0199
1-4	0.0450	2-4	0.0411	3-4	0.0267			5-4	0.0247	6-4	0.0187
1-5	0.0447	2-5	0.0425	3-5	0.0266	4-5	0.0240			6-5	0.0188
1-6	0.0364	2-6	0.0341	3-6	0.0227	4-6	0.0194	5-6	0.0197

見方は先ほどの表と同じです。
大分めりはりが出て来ました。さっきよりかはいい全然いい感じですね。
他のレースだとどうなのか、みてみたいですね。
先ほどのは、全レースの結果をまとめたのが悪かったのか、集計の仕方が間違えていたのか、モデルが悪いのか、理解が足りないのか、サンプリング数が足りていなかったのか。
もうちょっと勉強します。

次は、レースの予測方法を $\mu_n[n[g,r]]+\mu_c[c[g,r]]$ の中央値の大きさとしてみます。
結果は以下です。

		2-1	0.1071	3-1	0.0445	4-1	0.0320	5-1	0.0207	6-1	0.0155
1-2	0.1907			3-2	0.0294	4-2	0.0172	5-2	0.0126	6-2	0.0080
1-3	0.1178	2-3	0.0405			4-3	0.0138	5-3	0.0091	6-3	0.0073
1-4	0.0825	2-4	0.0298	3-4	0.0183			5-4	0.0093	6-4	0.0061
1-5	0.0599	2-5	0.0220	3-5	0.0096	4-5	0.0087			6-5	0.0054
1-6	0.0485	2-6	0.0151	3-6	0.0070	4-6	0.0066	5-6	0.0050

二連単的中率0.1907、二連複的中率0.2978ですね。いい感じですね。
ただこっちの予測方法だと、オッズが適正なのかどうかが分からない。困った。
でも、いい感じだったので、三連単の予測結果も見てみます。

		2-1-3	0.039	3-1-2	0.019	4-1-2	0.011	5-1-2	0.007	6-1-2	0.005
		2-1-4	0.029	3-1-4	0.012	4-1-3	0.008	5-1-3	0.007	6-1-3	0.004
		2-1-5	0.024	3-1-5	0.008	4-1-5	0.007	5-1-4	0.004	6-1-4	0.003
		2-1-6	0.016	3-1-6	0.006	4-1-6	0.005	5-1-6	0.003	6-1-5	0.003
1-2-3	0.073			3-2-1	0.015	4-2-1	0.011	5-2-1	0.007	6-2-1	0.004
1-2-4	0.053			3-2-4	0.006	4-2-3	0.003	5-2-3	0.002	6-2-3	0.002
1-2-5	0.033			3-2-5	0.005	4-2-5	0.002	5-2-4	0.002	6-2-4	0.001
1-2-6	0.031			3-2-6	0.004	4-2-6	0.002	5-2-6	0.002	6-2-5	0.001
1-3-2	0.056	2-3-1	0.021			4-3-1	0.006	5-3-1	0.004	6-3-1	0.003
1-3-4	0.028	2-3-4	0.007			4-3-2	0.004	5-3-2	0.003	6-3-2	0.002
1-3-5	0.018	2-3-5	0.007			4-3-5	0.003	5-3-4	0.002	6-3-4	0.002
1-3-6	0.016	2-3-6	0.005			4-3-6	0.002	5-3-6	0.001	6-3-5	0.001
1-4-2	0.031	2-4-1	0.014	3-4-1	0.008			5-4-1	0.004	6-4-1	0.003
1-4-3	0.027	2-4-3	0.007	3-4-2	0.006			5-4-2	0.003	6-4-2	0.001
1-4-5	0.015	2-4-5	0.006	3-4-5	0.003			5-4-3	0.002	6-4-3	0.001
1-4-6	0.009	2-4-6	0.003	3-4-6	0.002			5-4-6	0.001	6-4-5	0.001
1-5-2	0.022	2-5-1	0.011	3-5-1	0.004	4-5-1	0.004			6-5-1	0.001
1-5-3	0.016	2-5-3	0.005	3-5-2	0.003	4-5-2	0.003			6-5-2	0.002
1-5-4	0.014	2-5-4	0.004	3-5-4	0.001	4-5-3	0.001			6-5-3	0.001
1-5-6	0.008	2-5-6	0.003	3-5-6	0.001	4-5-6	0.001			6-5-4	0.001
1-6-2	0.019	2-6-1	0.006	3-6-1	0.003	4-6-1	0.003	5-6-1	0.001
1-6-3	0.012	2-6-3	0.004	3-6-2	0.002	4-6-2	0.002	5-6-2	0.002
1-6-4	0.011	2-6-4	0.003	3-6-4	0.001	4-6-3	0.001	5-6-3	0.001
1-6-5	0.007	2-6-5	0.003	3-6-5	0.001	4-6-5	0.001	5-6-4	0.001